In multicomplex dynamics, the Tetrabrot[1] is a 3D generalization of the Mandelbrot set. Discovered by Dominic Rochon in 2000, it can be interpreted as a 3D slice \(\mathcal{T}^2(1, \mathbf{i_1}, \mathbf{i_2})\) of the tricomplex Multibrot set \(\mathcal{M}_3^2\).
There are different algorithms to generate pictures of the Tetrabrot. In the tricomplex space, the algorithms use the tricomplex function \(f_c (\eta) := \eta^p + c \), where \(\eta , c \in \mathbb{TC}\) and \(p \geq 2\) is an integer. The number \(c \in \mathcal{T}^2 (1, \mathbf{i_1}, \mathbf{i_2})\) if and only if \(|f_c^m(0)| \leq 2\), for any integer \(m \geq 1\). This condition means that the set of all numbers \( f_c^m (0) \) should be bounded for every integer \(m \geq 1 \).
Since it is impossible to compute infinitely many iterations in a computer, we have to consider an approximation of the condition. Therefore, we fix a finite number of iterations to test, say \(M\). The number \(c\) belongs to the Tetrabrot if the numbers \(f_c^m(0)\), for \(m \in \{1, 2, \ldots , M\}\), remain bounded by \(2\). This is called the Divergence-Layer Algorithm. It is used to draw the Tetrabrot in the 3D space.
The tricomplex filled-in Julia set of order \(p = 2\), for \(c \in \mathbb{TC}\) is defined as $$ \mathcal{K}_{3, c}^2 := \{ \eta \in \mathbb{TC} \, : \, \{ f_c^m (\eta)\}_{m = 1}^\infty \text{ is bounded.} \} $$ The basin of attraction at \(\infty\) of \(f_c(\eta) = \eta^2 + c\) is defined as \(A_{3, c} (\infty) := \mathbb{TC} \backslash \mathcal{K}_{3, c}^2\), that is $$ A_{3, c} (\infty) = \{ \eta \in \mathbb{TC} \, : \, f_c^m (\eta ) \rightarrow \infty \text{ as } \eta \rightarrow \infty \} $$ and the strong basin of attraction at \(\infty\) of \(f_c\) as $$ SA_{3, c} (\infty ) := \Big( A_{c_{\gamma{1} \gamma_3}} (\infty) \times_{\gamma_1} A_{c_{\overline{\gamma}_1 \gamma_3}} (\infty ) \Big) \times_{\gamma_3} \Big( A_{c_{\gamma_1 \overline{\gamma}_3}} (\infty) \times_{\gamma_1} A_{c_{\overline{\gamma}_1 \overline{\gamma}_3}} (\infty) \Big) , $$ where \(A_c (\infty)\) is the basin of attraction of \(f_c\) at \(\infty\) for \(c \in \mathbb{C}(\mathbf{i_1})\).
With these notations, the generalized Fatou-Julia Theorem for \(\mathcal{M}_3^2\) is expressed in the following way[2]:
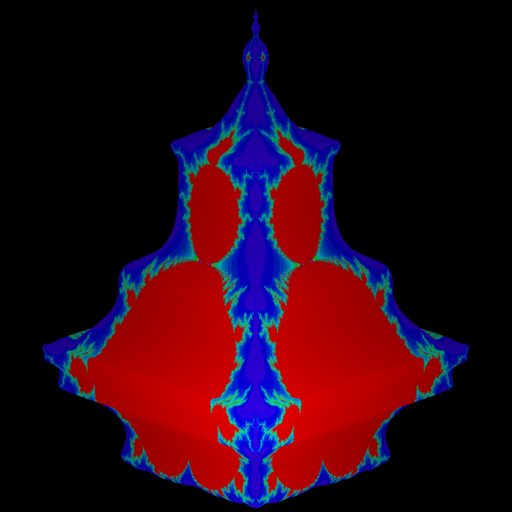
In 1982, A. Norton[3] gave some algorithms for the generation and display of fractal shapes in 3D. For the first time, iteration with quaternions[4] appeared. Theoretical results have been treated for the quaternionic Mandelbrot set[5][6] (see video) defined with quadratic polynomial in the quaternions of the form \(q^2 + c\).
In 2005, using bicomplex numbers, É. Martineau and D. Rochon[7] obtained estimates for the lower and upper bounds of the distance from a point \(c\) outside of the bicomplex Mandelbrot set \(\mathcal{M}_2^2\) to \(\mathcal{M}_2^2\) itself. Let \(c \not\in \mathcal{M}_2^2\) and define $$ d(c, \mathcal{M}_2^2) := \inf \{ |w - c| \, : \, w \in \mathcal{M}_2^2 .\} $$ Then, we have $$ d(c, \mathcal{M}_2^2) = \sqrt{\frac{d(c_{\gamma_1}, \mathcal{M}^2) + d(c_{\overline{\gamma}_1}, \mathcal{M}^2)}{2}}, $$ where \(\mathcal{M}^2\) is the standard Mandelbrot set.
Using the Green function \(G : \mathbb{C}(\mathbf{i_1}) \backslash \mathcal{M}^2 \rightarrow \mathbb{C}(\mathbf{i_1}) \backslash \overline{B}_1 (0, 1)\) in the complex plane, where \(\overline{B}_1 (0, 1)\) is the closed unit ball of \(\mathbb{C}(\mathbf{i_1}) \simeq \mathbb{C}\), the distance is approximated in the following way[8]: $$ \frac{|z_m| \ln |z_m|}{2|z_m|^{1/2^m} |z_m'|} \approx \frac{\sinh G(c_\gamma)}{2^{G(c_\gamma)}|G'(c_\gamma)|} < d(c_\gamma, \mathcal{M}^2) , $$ for any \(c_\gamma \in \mathbb{C}(\mathbf{i_1}) \backslash \mathcal{M}^2\) and for large \(m\), where \(z_m := f_{c_\gamma}^m (0)\) and \(z_m' := \frac{d}{dc} f_c (0) |_{c = c_\gamma}\). This approximation gives a lower bound that can be used to ray-trace the Tetrabrot.
There exists also a generalization of the lower bound for \(d (c, \mathcal{M}_2^2)\) to the tricomplex Multibrot set of order \(p\)[9]. Some ressources and images can be found on the Aleph One's personal page. There is also a video available on Youtube, where specific regions of the Rochon's Tetrabrot are explored.