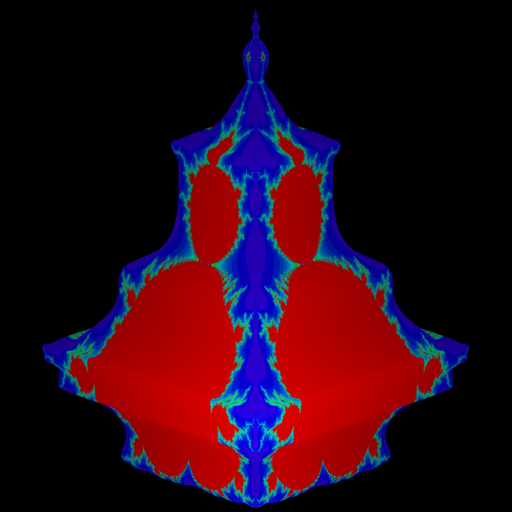
En dynamique multicomplexe, le Tétrabrot^[1] est une généralisation tridimensionnelle de l’ensemble de Mandelbrot. Découvert par Dominic Rochon en 2000, il peut être interprété comme une tranche tridimensionnelle ${\mathcal{T}}^2(1,{\mathbf{i}}_{\mathbf{1}},{\mathbf{i}}_{\mathbf{2}})$ de l’ensemble Multibrot tricomplexe ${\mathcal{M}}_3^2$.

Algorithme par couches de divergence

Il existe différents algorithmes permettant de générer des images du Tétrabrot. Dans l’espace tricomplexe, ces algorithmes utilisent la fonction tricomplexe $f_c(\eta ):={\eta }^p+c$, où $\eta ,c\in \mathbb{TC}$ et où $p\ge 2$ est un entier. Le nombre $c$ appartient à ${\mathcal{T}}^2(1,{\mathbf{i}}_{\mathbf{1}},{\mathbf{i}}_{\mathbf{2}})$ si et seulement si $|f_c^m(0)|\le 2$, pour tout entier $m\ge 1$. Cette condition signifie que l’ensemble des nombres $f_c^m(0)$ doit être borné pour tout entier $m\ge 1$.

Puisqu’il est impossible de calculer un nombre infini d’itérations sur un ordinateur, il est nécessaire de considérer une approximation de cette condition. On fixe donc un nombre fini d’itérations à tester, disons $M$. Le nombre $c$ appartient au Tétrabrot si les nombres $f_c^m(0)$, pour $m\in \{1,2,\dots ,M\}$, demeurent bornés par $2$. Cette méthode est appelée algorithme par couches de divergence (*Divergence-Layer Algorithm*). Elle est utilisée pour tracer le Tétrabrot dans l’espace tridimensionnel.

Illustration du Tétrabrot à l’aide de l’algorithme par couches de divergence

Théorème de Fatou-Julia généralisé

L’ensemble de Julia rempli tricomplexe d’ordre $p=2$, pour $c\in \mathbb{TC}$, est défini par $${\mathcal{K}}_{3,c}^2:=\{\eta \in \mathbb{TC}:\{f_c^m(\eta ){\}}_{m=1}^{\mathrm{\infty }}\text{ est bornée.}\}$$ Le bassin d’attraction en $\mathrm{\infty }$ de $f_c(\eta )={\eta }^2+c$ est défini par $A_{3,c}(\mathrm{\infty }):=\mathbb{TC}\mathrm{\setminus }{\mathcal{K}}_{3,c}^2$, c’est-à-dire $$A_{3,c}(\mathrm{\infty })=\{\eta \in \mathbb{TC}:f_c^m(\eta )\to \mathrm{\infty }\text{ lorsque }m\to \mathrm{\infty }\}$$ et le bassin d’attraction fort en $\mathrm{\infty }$ de $f_c$ est défini par $$S{A}_{3,c}(\mathrm{\infty }):=(A_{c_{\gamma 1{\gamma }_3}}(\mathrm{\infty }){\times }_{{\gamma }_1}{A}_{c_{{\bar{\gamma }}_1{\gamma }_3}}(\mathrm{\infty })){\times }_{{\gamma }_3}(A_{c_{{\gamma }_1{\bar{\gamma }}_3}}(\mathrm{\infty }){\times }_{{\gamma }_1}{A}_{c_{{\bar{\gamma }}_1{\bar{\gamma }}_3}}(\mathrm{\infty })),$$ où $A_c(\mathrm{\infty })$ désigne le bassin d’attraction de $f_c$ en $\mathrm{\infty }$ pour $c\in \mathbb{C}({\mathbf{i}}_{\mathbf{1}})$.

Avec ces notations, le théorème de Fatou-Julia généralisé pour ${\mathcal{M}}_3^2$ s’énonce de la manière suivante^[2] :

• $0\in {\mathcal{K}}_{3,c}^2$ si et seulement si ${\mathcal{K}}_{3,c}^2$ est connexe ;
• $0\in S{A}_{3,c}(\mathrm{\infty })$ si et seulement si ${\mathcal{K}}_{3,c}^2$ est un ensemble de Cantor ;
• $0\in A_{3,c}(\mathrm{\infty })\mathrm{\setminus }S{A}_{3,c}(\mathrm{\infty })$ si et seulement si ${\mathcal{K}}_{3,c}^2$ est déconnecté mais pas totalement.

Illustration du théorème de Fatou-Julia pour le Tétrabrot

Lancer de rayons

En 1982, A. Norton^[3] a proposé plusieurs algorithmes pour la génération et l’affichage de formes fractales en trois dimensions. Pour la première fois, l’itération utilisant des quaternions^[4] est apparue. Des résultats théoriques ont été obtenus pour l’ensemble de Mandelbrot quaternionique^[5][6] (voir la vidéo), défini à l’aide du polynôme quadratique quaternionique $q^2+c$.

Ensemble de Julia quaternionique avec paramètres $c=0.123+0.745i$ et une coupe dans le plan $XY$. L’ensemble de Julia « Douady Rabbit » est visible dans la coupe.

En 2005, en utilisant les nombres bicomplexes, É. Martineau et D. Rochon^[7] ont obtenu des estimations des bornes inférieure et supérieure de la distance entre un point $c$ situé à l’extérieur de l’ensemble de Mandelbrot bicomplexe ${\mathcal{M}}_2^2$ et ${\mathcal{M}}_2^2$ lui-même. Soit $c\notin {\mathcal{M}}_2^2$, et définissons $$d(c,{\mathcal{M}}_2^2):=inf\{|w-c|:w\in {\mathcal{M}}_2^2.\}$$ Alors, $$d(c,{\mathcal{M}}_2^2)=\sqrt{\frac{d(c_{{\gamma }_1},{\mathcal{M}}^2)+d(c_{{\bar{\gamma }}_1},{\mathcal{M}}^2)}{2}},$$ où ${\mathcal{M}}^2$ désigne l’ensemble de Mandelbrot classique.

En utilisant la fonction de Green $G:\mathbb{C}({\mathbf{i}}_{\mathbf{1}})\mathrm{\setminus }{\mathcal{M}}^2\to \mathbb{C}({\mathbf{i}}_{\mathbf{1}})\mathrm{\setminus }{\bar{B}}_1(0,1)$ dans le plan complexe, où ${\bar{B}}_1(0,1)$ est la boule unité fermée de $\mathbb{C}({\mathbf{i}}_{\mathbf{1}})\simeq \mathbb{C}$, la distance est approximée de la manière suivante^[8] : $$\frac{|z_m|\ln |z_m|}{2|z_m{|}^{1/2^m}|z_m^{\prime }|}\approx \frac{\sinh G(c_{\gamma })}{2^{G(c_{\gamma })}|G^{\prime }(c_{\gamma })|}<d(c_{\gamma },{\mathcal{M}}^2),$$ pour tout $c_{\gamma }\in \mathbb{C}({\mathbf{i}}_{\mathbf{1}})\mathrm{\setminus }{\mathcal{M}}^2$ et pour $m$ suffisamment grand, où $z_m:=f_{c_{\gamma }}^m(0)$ et $z_m^{\prime }:=\frac{d}{dc}{f}_c(0){|}_{c=c_{\gamma }}$. Cette approximation fournit une borne inférieure pouvant être utilisée pour le lancer de rayons du Tétrabrot.

Tétrabrot obtenu par lancer de rayons

Il existe également une généralisation de la borne inférieure pour $d(c,{\mathcal{M}}_2^2)$ à l’ensemble Multibrot tricomplexe d’ordre $p$^[9]. Certaines ressources et images sont disponibles sur la page personnelle de Aleph One. Une vidéo est également disponible sur YouTube, où des régions spécifiques du Tétrabrot de Rochon sont explorées.

Références

1. ^D. Rochon, « A Generalized Mandelbrot Set for Bicomplex Numbers », Fractals, 8(4):355-368, 2000.
2. ^V. Garant-Pelletier et D. Rochon, « On a Generalized Fatou-Julia Theorem in Multicomplex Space », Fractals, 17(3):241-255, 2008.
3. ^A. Norton, « Generation and Display of Geometric Fractals in 3-D », Computer Graphics, 16:61-67, 1982.
4. ^I. L. Kantor, Hypercomplex Numbers, Springer-Verlag, New-York, 1982.
5. ^S. Bedding et K. Briggs, « Iteration of Quaternion Maps », Int. J. Bifur. Chaos Appl. Sci. Eng., 5:877-881, 1995.
6. ^J. Gomatam, J. Doyle, B. Steves et I. McFarlane, « Generalization of the Mandelbrot Set: Quaternionic Quadratic Maps », Chaos, Solitons & Fractals, 5:971-985, 1995.
7. ^É. Martineau et D. Rochon, « On a Bicomplex Distance Estimation for the Tetrabrot », International Journal of Bifurcation and Chaos, 15(6):501-521, 2005.
8. ^J. C. Hart, D. J. Sandin et L. H. Kauffman, « Ray tracing deterministic 3-D fractals », Comput. Graph., 23:289-296, 1989.
9. ^G. Brouillette, P.-O. Parisé et D. Rochon, « Tricomplex Distance Estimation for Filled-in Julia Sets and Multibrot Sets », International Journal of Bifurcation and Chaos, 29(6), 2019.